E 無理数 証明 553142-E 無理数 証明 阪大
なぜわかっていないかは証明されていないからでしょうが、直感的に無理数といいうのであれば、 e i π = − 1 も直感的には無理数になりそうですが、きれいな数値になりますよね。Eが無理数であることの証明 この小論は,「eは無理数である」ことを,高校の数学を学んだ生徒に理解しやすいような形で 証明することを目的としている. 1 準備 1.1 無限級数の和について この小論に登場する無限級数は,すべて和を持つものだけであることを断っておく.π e π は、ネステレンコ (enYuri Valentinovich Nesterenko) によって無理数であることが証明された。 未解決の問題 オイラー定数 γ , π e , e π , その他 P ( e , π )( P ( X , Y ) は X , Y 双方について次数が 1 以上である多項式)は有理数であるか無理数であるか知られ
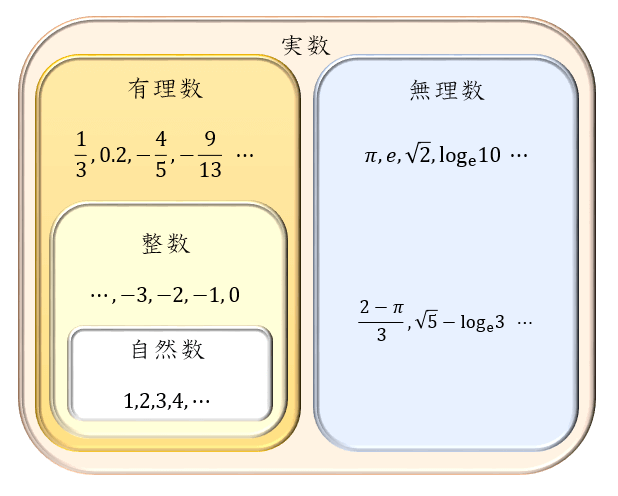
自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ
E 無理数 証明 阪大
E 無理数 証明 阪大-6 証明問題有理数と無理数について 7 √3が無理数であることを既知として、√3√5が無理数であることを証明せよ。「閉じていることを」利用 8 高1の数学Ⅰです。 背理法を用いて√2が無理数であることを証明するのですが 証明 √2は無理数でなぜわかっていないかは証明されていないからでしょうが、直感的に無理数といいうのであれば、 e i π = − 1 も直感的には無理数になりそうですが、きれいな数値になりますよね。



証明 自然対数の底 E は無理数である 理数系無料オンライン学習 Kori
√2が無理数であることの証明 その1 √2が有理数であると仮定する。つまり\( \sqrt{2}=\frac{n}{m} \)と書けるとする。 整理すると2m 2 =n 2 左辺は2で奇数回割り切れるが,右辺は2で偶数回割り切れる。 よって両辺が等しいことに矛盾。背理法より√2は無理数Eが無理数であることの証明(オイラー) 実は e が無理数であることは1737年にオイラーによって初めて証明されました。 (論文に掲載されたのは1744年) オイラーの証明は無限連分数展開を用いるものです。 (2の証明が発見できませんでした。 発見した方はご一報ください。 方針: 1:有理数なら正則連分数展開は有限回で終わる 2: e は正則連分数展開が無限定理1 (Ch Hermite(エルミート), 1873) e は超越数である 注意Ian Stewart の証明がM に載っていて, 以下の証明はそれを転 記したものである 証明背理法を用いて示そう(e が代数的数であると仮定して矛盾を導 く) 今自然数m と整数a0 (̸= 0), a1, ···, am を (4) a0em a1em
Eが無理数であることの証明 e が有理数であると仮定すると、 ( p , q は自然数) と表される。いま、 は整数となるが、(4)の結果に反する。よって背理法により、 e は無理数であることが示された。 eを無限和で表すすなわち e は無理数 である . 4πが無理数 である 証明 eに比べると ,πが無理数 である 証明 は少々込み入っている 。その 理由 はよく 分からな いが 、e よりも πの方が数としての 構造 がより 複雑 なのかもしれない 。最初 にπが無理数2 は無理数である。 2 は無理数ではない、すなわち有理数であると仮定すると、 互いに素である自然数a, bを用いて 2 = b a と表すことができる。 これを変形して b = 2 a 両辺を2乗して b 2 = 2a 2 ・・・(1) b 2 は偶数となるので、①よりbも偶数である。
\(e\) が無理数であることの証明 以下の証明は@von_archimedeanさんのツイートを自分の理解のために清書したものです。 https無理数同士の和も直接証明しなくて済む理解の仕方あるかね 18 132人目の素数さん (月) IDx2ECopLe 片方だけ適当に代数的数を足せばいい理数をであることを示した方がいいと思ったが、より簡単なeが無理数であることを証明した。 今日、 e^2 ,e^3, ・・・, e^n π^2, π^3, ・・・, π^n (nは自然数) すべてが無理数であることがわかっている。



ブログ 15の最も有名な超越数



証明 自然対数の底 E は無理数である 理数系無料オンライン学習 Kori
Eのべき(有理数乗)が無理数であることの証明 この証明は概要だけ書いておく。 を整数()とするとき、 が無理数であることを示す。このとき、 なら 、 と置き直しても の値は変わらないので、 としてよい。 有理数の整数乗は有理数であることから、 が有理数なら は有理数。無理数同士の和も直接証明しなくて済む理解の仕方あるかね 18 132人目の素数さん (月) IDx2ECopLe 片方だけ適当に代数的数を足せばいいすなわち e は無理数 である . 4πが無理数 である 証明 eに比べると ,πが無理数 である 証明 は少々込み入っている 。その 理由 はよく 分からな いが 、e よりも πの方が数としての 構造 がより 複雑 なのかもしれない 。最初 にπが無理数



背理法と対偶命題の証明法は どのように使い分けるのか 東大合格 敬天塾


大学数学の有理数 無理数の稠密性の証明問題と 連続関数に関する問題 Yahoo 知恵袋
これは e が既約分数で表せると仮定したことによる矛盾であり、よって e は無理数であることが背理法にて証明された。 2人 がナイス! していますネイピア数の無理性の証明(ねいぴあすうのむりせいのしょうめい)は、1744年にオイラーが初めて行った。実際、ネイピア数 e は 2 < e < 3 を満たす無理数である。証明は背理法による。すなわち、 e が有理数であると仮定して矛盾を導く。これは e が既約分数で表せると仮定したことによる矛盾であり、よって e は無理数であることが背理法にて証明された。 2人 がナイス! しています



無理数乗 と 虚数乗 数学って面白い



背理法についてです 単純な背理法の証明の仕方は習って ほとん 高校数学に関する質問 勉強質問サイト
自然対数の底 e が無理数である証明以前の記事で, 円周率\(\pi\)が無理数, つまり (整数) / (整数) と分数の形では表せない証明として, Nivenの方法を紹介しました今回は, 自然対数の底 \(e\) が無理数である証明を無理数を指数とする累乗の定義の具体例 無理数πを指数とする累乗a π は、以下のように定義される。 step0 無理数πを小数で表す。 π= よく知られているように、無理数は、循環しない無限小数で表される。自然対数の底 e が無理数である証明以前の記事で, 円周率\(\pi\)が無理数, つまり (整数) / (整数) と分数の形では表せない証明として, Nivenの方法を紹介しました今回は, 自然対数の底 \(e\) が無理数である証明を
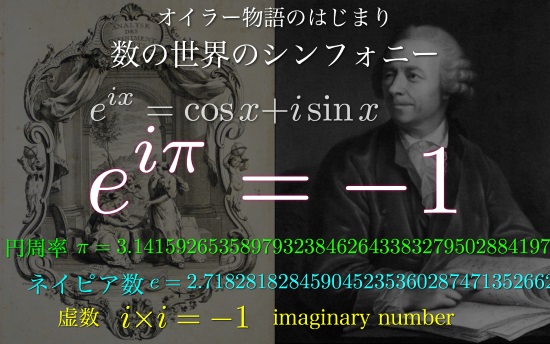


オイラーの公式 三角関数 複素指数関数 虚数が等式として集約されるまでの物語 空間情報クラブ 株式会社インフォマティクス



添削をお願いしたいです 設問は2です図示後の また のと 高校数学に関する質問 勉強質問サイト
無理数同士の和も直接証明しなくて済む理解の仕方あるかね 18 132人目の素数さん (月) IDx2ECopLe 片方だけ適当に代数的数を足せばいいπ e π は、ネステレンコ (enYuri Valentinovich Nesterenko) によって無理数であることが証明された。 未解決の問題 編集 オイラー定数 γ , π e , e π , その他 P ( e , π )( P ( X , Y ) は X , Y 双方について次数が 1 以上である多項式)は有理数であるか無理数である
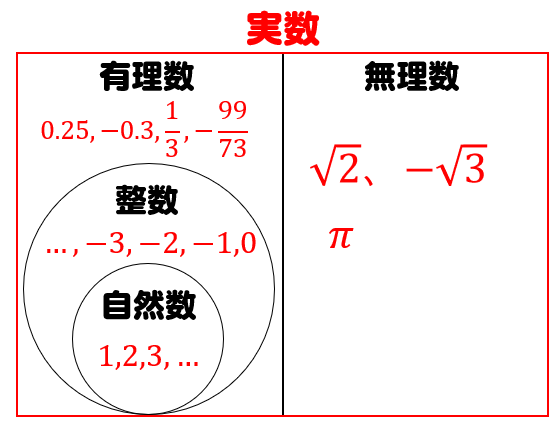


有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun



無理数と超越数 塩川 宇賢 本 通販 Amazon


東大数学専科典型題演習34 マクローリン展開



超越数とは何か 自然対数の底eや円周率pが超越数である証明を解説 超越数一覧もあり 遊ぶ数学


Grb1f Htm



sシラバス



応用 対数と無理数 なかけんの数学ノート


0の0乗ってなんなの 0乗だから1になる 数学の面白いこと 役に立つことをまとめたサイト



自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ



ネイピア数の無理性の証明 Proof That E Is Irrational Japaneseclass Jp



円周率とラマヌジャン Qiita
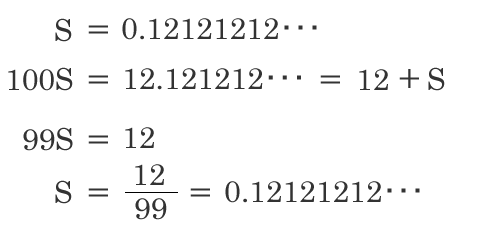


2が無理数である証明 実数 有理数 無理数 優技録



極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室


無理数の無理数乗は無理数か Tsujimotterのノートブック



Eが無理数であることの証明 数学の偏差値を上げて合格を目指す



2 のところに 1 の結果からとありますが 2 と1 はどう関係があるのでしょう Clear



E が無理数であることの証明 1997 大阪大 理 後 イズミの数学



無理数の無理数乗は無理数か Tsujimotterのノートブック



背理法とは 無理数の問題例と証明を徹底解説 理系ラボ



有理数と無理数2 有理数の稠密性を中心として 身勝手な主張



55期生通信 Elcas11 Report25



証明 自然対数の底 E は無理数である 理数系無料オンライン学習 Kori



Pが無理数であることの証明 身勝手な主張



数列 1 1 N N が収束することの証明 再掲載 身勝手な主張
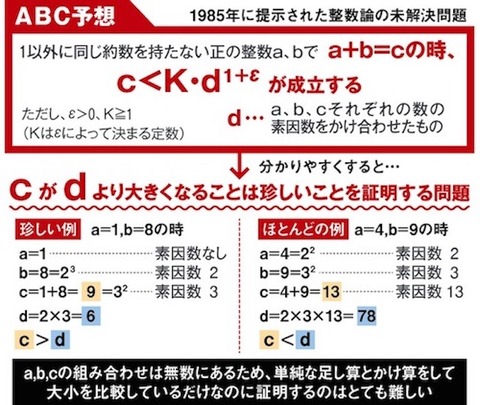


京都の 知 未解明だった数学の超難問 Abc予想 を証明 京大の望月新一 教授 斬新 難解で査読に8年 つれづれなるままの数学 算数 素数gpsの周辺 Iphoneとandroid 366 Aps
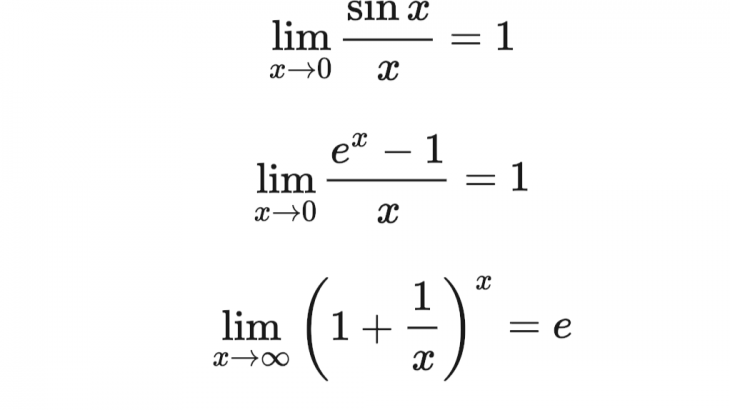


極限公式で覚えておくべきはたった3つ 証明 導出 覚え方を教えます 東大医学部生の相談室
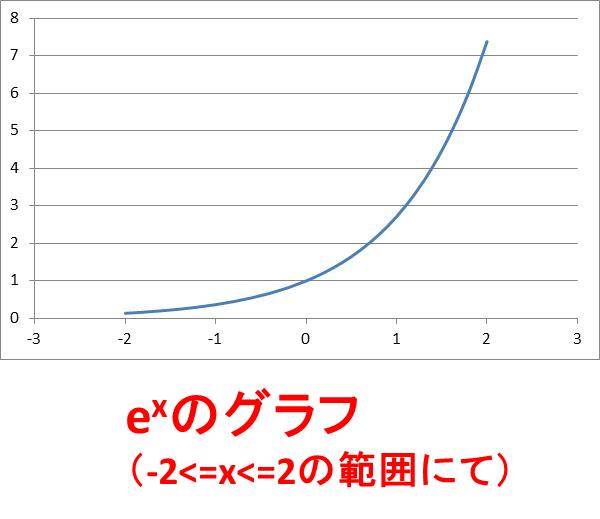


Eの0乗は値は何か Eの1乗やeのマイナス1乗 マイナス2乗の数値は y E 2xのe Xのグラフの書き方は エクセル ウルトラフリーダム



無理数とお友達になろう 第384回科学勉強会



証明 E P Ep のいずれかは無理数 アットランダム ブリコラージュ 転ぶな 風邪ひくな 義理を欠け 長寿の心得 岸信介 食う 寝る 出す 風呂 在宅生活4つの柱



Eが無理数であることの証明 身勝手な主張



背理法と有理数 無理数の証明 高校数学 Youtube



E が無理数であることの証明 1997 大阪大 理 後 イズミの数学



高校数学 Eについて 1 映像授業のtry It トライイット



有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri



コロちゃんぬ この証明めっちゃ好きなんだけど Fltの証明内に2のn乗根が無理数であること およびそれを用いて証明される命題 を使ってたら循環論法になっちゃうけど 大丈夫なのかな



有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun



関数の単調性の証明 いろいろな方法で示してみよう 身勝手な主張


03年入試問題研究



バーゼル問題とは 東工大入試にも出てきた問題を証明 円周率に収束 遊ぶ数学



高校数学 Eについて 1 映像授業のtry It トライイット



2 のところに 1 の結果からとありますが 2 と1 はどう関係があるのでしょう Clear


Grb1f Htm
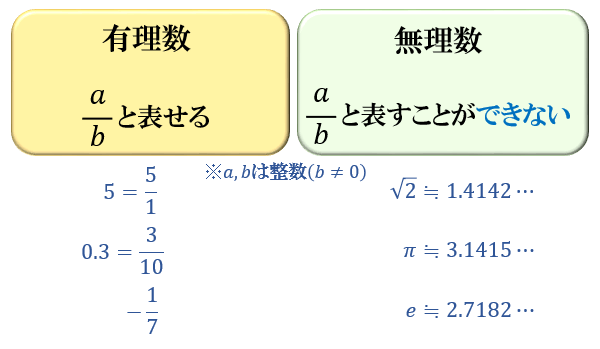


有理数と無理数の違い ルート2が無理数であることの証明 アタリマエ



自然対数 Ln 自然対数の底 E とは 定義や微分積分の計算公式 受験辞典


11 有理数 無理数の問題 京極一樹の数学塾


二次試験の数学が楽しい なべのおしらせブログ Powered By なべブロ
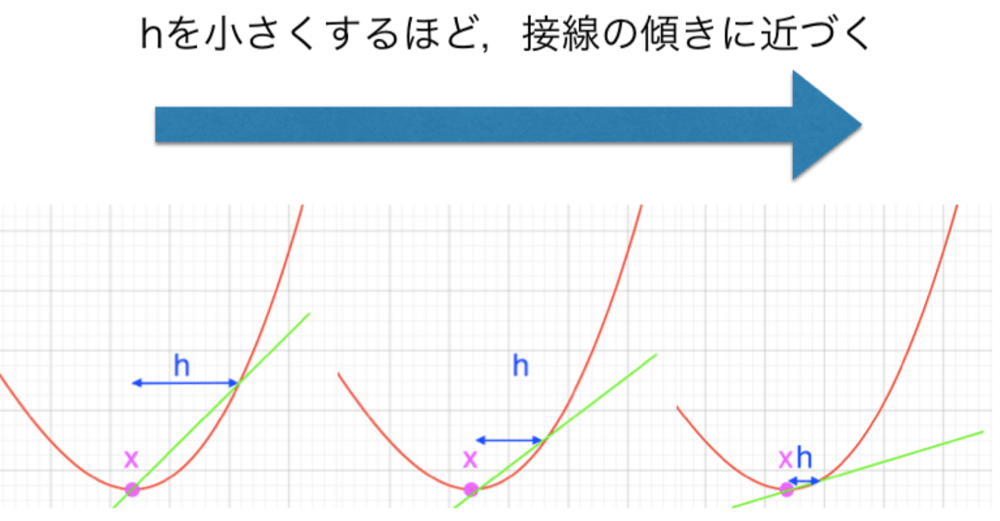


ネイピア数eの定義がなぜあの形か 先生は説明をしてくれなかった ロボット It雑食日記



べき乗とは何か ゼロ乗 マイナス乗 分数乗 無理数乗ってどういう意味 アタリマエ


数と式 思考力を鍛える数学


無理数 Wikipedia



無理数とお友達になろう 第384回科学勉強会



無理数とお友達になろう 第384回科学勉強会


情報数学 1回目



無理数であることの証明 数学の偏差値を上げて合格を目指す
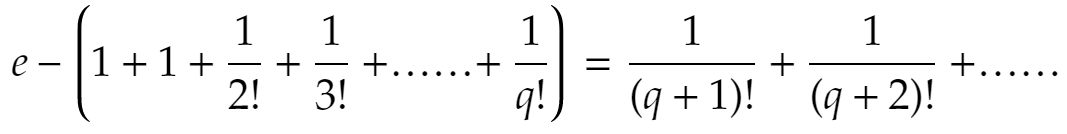


自然対数の底 E は無理数であることの証明 いぬおさんのおもしろ数学実験室


この 1 って模範解答では対偶を証明しているのですが 背理法 Yahoo 知恵袋


ネイピア数の無理性の証明 Proof That E Is Irrational Japaneseclass Jp



福井大学 医学部 14年問題4 Suugaku Jp


ネイピア数の表現 Wikipedia


三石 数学塾 ルート2が無理数であること



無理数 無理数 無理数 なつれ Note



ルート3が無理数であることを証明せよ 世界変動展望



本書で紹介する定理たち Hirosi Ooguri



数学 37 第2章 集合と命題 4 B 背理法を利用する証明 Youtube



第2話 補遺 Hirosi Ooguri


鹿児島大学 教育学部 14年問題1 Suugaku Jp



55期生通信 Elcas11 Report25
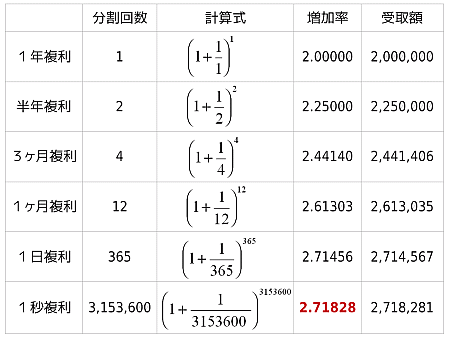


数列 連続複利とネイピア数 E 大人が学び直す数学
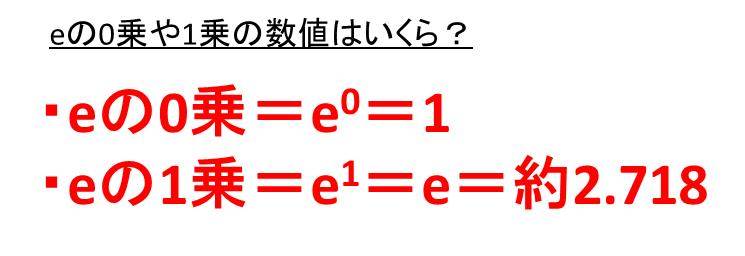


Eの0乗は値は何か Eの1乗やeのマイナス1乗 マイナス2乗の数値は y E 2xのe Xのグラフの書き方は エクセル ウルトラフリーダム



2 3 5 7は無理数である など Integers



数学科女子が 3 14小説 に挑戦 Pが導くラブストーリー Lab On ブルーバックス 講談社 3 3


11 有理数 無理数の問題 京極一樹の数学塾



人気の ネイピア数 動画 11本 ニコニコ動画



Eが超越数であることの証明 Youtube



有理数 無理数とは 違いを簡単に解説 中学生が覚えるべき無理数は2種類だけ 数学fun



無理数乗 の不思議 数学って面白い


三石 数学塾 ルート2が無理数であること


Pは無理数 の証明 怜悧玲瓏 高校数学を天空から俯瞰する



3 4 E 2 718 Q 1 2 がわかりま 高校数学に関する質問 勉強質問サイト



アドカレ 好きな証明 無理数論 散れども切れぬ備忘録


11 有理数 無理数の問題 京極一樹の数学塾


高1数学の背理法について この問題で 3は有理数と仮定する場 Yahoo 知恵袋


03年入試問題研究


11 有理数 無理数の問題 京極一樹の数学塾


オイラーの公式をテイラー展開で証明する



テイラーの定理の証明と応用



実数の分類 有理数 無理数とは何か 数学を極めるsukimonograph


情報数学 2回目



この写真の赤ラインのとこなんですけど 証明するときに R 有理数 ってするときと Clear



高校生も納得 テイラー展開 マクローリン展開の証明と使い方 高校生向け受験応援メディア 受験のミカタ
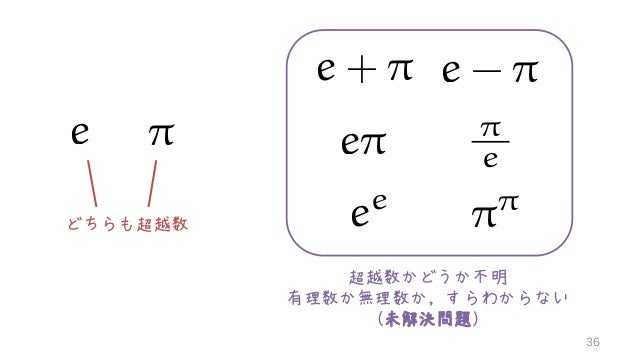


無理数とお友達になろう 第384回科学勉強会



有理数とは 無理数とは 定義を明らかにして が無理数と証明する 数学ia Himokuri
コメント
コメントを投稿